Das Modul zur Korrelation ist eine wertvolle Unterstützung, um Korrelationen zwischen Schwingungswerten und Prozessparametern bei virtuellen Trends aufzuzeigen. Dies ist vor allem dann sinnvoll, wenn die Schwingungskennwerte der Anlage von einem Prozessparameter abhängen, aber damit kein Zusammenhang mit einem Schaden besteht. Sobald ein Bauteil auf die dafür vorgesehene Arbeitsfläche vom Korrelationsfenster gezogen wird, werden alle Trends geladen, die unter diesem Bauteil vorhanden sind.
Hinweis:
Wenn ein Bauteil einer hohen Ebene, wie z. B. eine Anlage oder eine Aggregatgruppe ausgewählt wird, kann die Anzahl der zugehörigen Trends sehr groß sein und damit auch die Ladezeit stark ansteigen. Wird die vordefinierte Anzahl der Trends überschritten, bricht der Ladevorgang ab. In diesem Fall können Sie diesen Wert erhöhen, oder Sie wählen ein Bauteil geringerer Ebene aus, z. B. eine Bauteilgruppe.
Filterparameter
Basierend auf den Filterparametern werden die Einträge angezeigt. Folgend sind die Parameter aufgelistet.
|
Von |
Das Startdatum für den Zeitbereich, der für die Berechnung der neuen Korrelationseinstellungen verwendet werden soll. Der Standardwert ist ein Monat in die Vergangenheit. |
|
Bis |
Das Enddatum für den Zeitbereich, der für die Berechnung der neuen Korrelationseinstellungen verwendet werden soll. Der Standardwert ist das aktuelle Datum. |
|
Regression |
Hier ist die Regressionsmethode gemeint. Bei der aktuellen Version kann nur „Linear regression“ ausgewählt werden. |
|
Korrelationssignal |
Auf dieses Feld kann von der Anlage ein Sensor gezogen werden. Die korrelierbaren Trends werden dann in der Liste unterhalb aufgelistet. Auswählbare Korrelationssignale:
|
|
Max. Trendanzahl |
Die maximale Anzahl an virtuellen Trends, die gleichzeitig geladen werden. Eventuell müssen Sie diesen Wert erhöhen, wenn Sie eine größere Anlageneinheit, z. B. Aggregat ausgewählt haben. |
|
Gesamtanzahl |
Zeigt die Anzahl der gefundenen virtuellen Trends zum gewählten Anlagenteil an. Hinweis: Wenn in einer der Spalten der Liste ein Filter gesetzt ist, kann die Anzahl der angezeigten Zeilen geringer als die Gesamtanzahl sein. |
|
Überschreiben erzwingen |
Durch Klicken des Buttons werden die alten Werte durch die neuen ersetzt. |
Bedeutung der Regressionsparameter für die lineare Regression
|
P1 |
Steigung der ermittelten Regressionsgerade |
|---|---|
|
P2 |
Maximalwert des Korrelationssignals im Berechnungszeitraum. Auf diesen Wert werden die virtuellen Trends umgerechnet. |
|
R^2 (R2) |
Dieser Parameter wird als Bestimmtheitsmaß bezeichnet und liegt zwischen 0 und 1. Höhere Werte bedeuten einen höheren linearen Zusammenhang und lassen auf eine höhere „Qualität“ der Regression schließen. 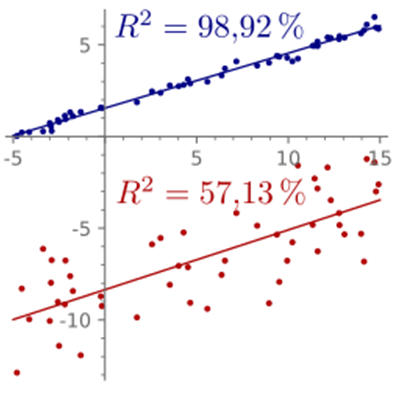 Quelle: https://commons.wikimedia.org/ Bei Werten über 0,5 kann die Regression eine Verbesserung der Trendwerte bringen (vor allem bei Trends, die aus der Hüllkurve berechnet werden, wie Wälzlager-Trends), bei Werten unter 0,5 sollte die Korrelation nicht verwendet werden. |
In den Spalten pP1, pP2 und pR^2 werden die Korrelationswerte von früheren Berechnungen angezeigt, sofern welche durchgeführt wurden. Sollten die berechneten Parameter nicht zufriedenstellend sein, können diese manuell bearbeitet werden. Aktivieren Sie dazu das Kontrollkästchen in der Spalte Benutzerdefiniert. Beim Klicken auf die Schaltfläche <Alle übernehmen> werden die neuen Werte dauerhaft abgespeichert. Über die Schaltfläche <Alle entfernen> werden diese Werte der Korrelationsberechnung ausgeschlossen. Die Trends selbst werden mit dieser Operation nicht gelöscht.
Egal wie viele virtuelle Trends im Hintergrund auch geladen sind, mit der Schaltfläche <Übernehme sichtbare Einträge> werden nur die in der Liste tatsächlich sichtbaren Werte übernommen. Alle anderen Grenzwerte bleiben unverändert.
Im Register Virtueller Trendtyp werden alle Trendtypen angezeigt, bei denen die Korrelation möglich ist. Die Trendtypen, die angehakt sind, werden für die Korrelation empfohlen.
Exkurs: Wie funktioniert die Korrelation?
Angenommen die Trendberechnung eines Schwingungssensors (z. B. ein RMS-Wert) hängt stark von der Motordrehzahl ab. In dem Fall erhöht sich der RMS-Pegel mit steigender Motordrehzahl und umgekehrt sinkt der RMS-Wert bei geringerer Motordrehzahl.
Dieser Umstand bedeutet, dass ein höherer RMS-Pegel nicht unbedingt gleich auf ein mechanisches Problem zurückzuführen ist. Um den RMS-Wert nun mit der Motordrehzahl zu "normieren", gibt es die CMU-Korrelation.
Anknüpfend am vorigen Beispiel geht man von zwei Signalen aus:
-
Die Motordrehzahl (auch bekannt als unabhängige Variable im statischen Begriff oder der X-Wert)
-
Der RMS-Wert (auch bekannt als abhängige Variable im statischen Begriff oder der Y-Wert)
Basierend auf diesen beiden Werten, berechnet man nun eine Linie, die am besten die Datenpunkte repräsentiert.
Diese Linie ist in der folgenden Abbildung violett gezeichnet. Die Berechnung liefert den Parameter P1, der die Steigung der Linie angibt, und den Parameter P2, der der höchsten gemessenen Motordrehzahl in den Datenpunkten entspricht, sowie den Wert R2, der einen Hinweis darauf gibt, wie gut die Linie die Datenpunkte repräsentiert.
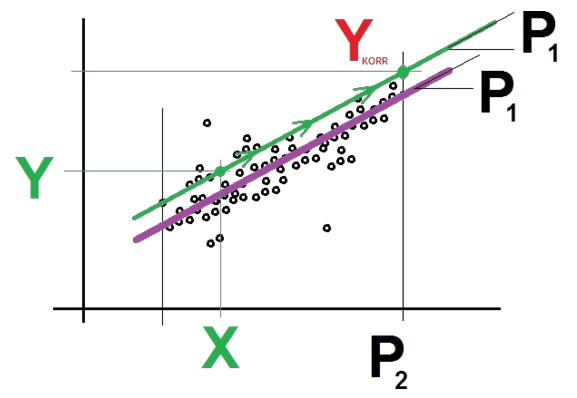
Beim Korrelationsverfahren beginnt die CMU mit einer neuen Berechnung des Schwingungssignals und der Motordrehzahl. Diese neuen Werte sind X und Y. Die CMU macht dann folgende Berechnung:
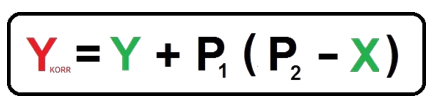
Durch die Berechnung erfolgt eine Verschiebung des original berechneten RMS-Wertes zu einem höheren RMS-Wert YKORR bei einer höheren Motordrehzahl P2. Dadurch wird im Prinzip vorgetäuscht, dass bei einer höheren Drehzahl gemessen worden ist.
Durch das Korrelationsprinzip wird der RMS-Trend um einiges glatter (weniger Varianz), da er nicht mehr so sehr von der Motordrehzahl abhängt.