Int('Expression',' Reset')
Argumente
|
'Expression' |
Messwert |
|
|
'Reset' |
Optionaler digitaler Parameter, der zum Rücksetzen des Integrals bzw. Unterdrücken des Integrationsvorgangs verwendet werden kann. 'Reset' kann selbst auch ein Ausdruck sein |
|
|
'Reset' > 0 |
Integral wird zurückgesetzt. |
|
|
'Reset' = 0 |
Integration freigegeben (Voreinstellung) |
|
Beschreibung
Diese Funktion liefert als Ergebnis das Integral (y * dt) von 'Expression' zurück. Der Parameter 'Reset' kann zum Rücksetzen des Integrals bzw. Unterdrücken des Integrationsvorgangs verwendet werden, z. B. um bei periodischen oder reversierenden Vorgängen dasselbe Signal mehrfach zu integrieren. 'Reset' kann selbst auch ein Ausdruck sein.
Beispiele:
|
Int([0:0]) |
Es erfolgt kein Reset ('Reset' weggelasen) |
|
Int([0:0],If(Mod(T(),20)=0,TRUE(),FALSE())) |
Das Integral wird alle 20 Sekunden zurückgesetzt. |
|
Int([0:0], [3.1]) |
z. B. mit [3.1] = If([0:0]>10, 1, 0) Das Integral wird zurückgesetzt, sobald der Ausdruck [3.1] TRUE zurückgibt, also wenn der Ausdruck [0:0] den Grenzwert 10 überschreitet. |
Beispiel 1
Tipp |
|
|---|---|
|
Diese Funktion kann in einem virtuellen Remanenzmodul verwendet werden. Ihre Ergebniswerte können damit über ein Stoppen und Neustarten der Messung erhalten werden. |
|
Ist 'Expression' ein Beschleunigungssignal so kann durch iteratives Ausführen der Int-Funktion daraus der zurückgelegte Weg ermittelt werden.
Aufgabenstellung
Mithilfe eines Beschleunigungssensors sollen die Geschwindigkeit sowie der zurückgelegte Weg bestimmt werden
Lösung
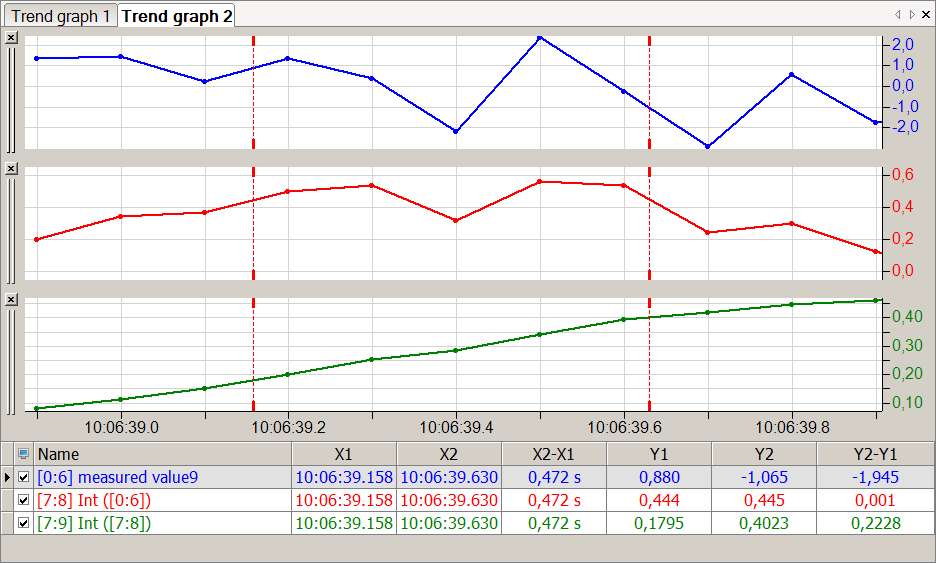
In der nachfolgenden Abbildung zeigt die blaue Kurve die gemessene Beschleunigung, die rote Kurve den berechneten Verlauf der Geschwindigkeit und die grüne Kurve die berechnete zurückgelegte Wegstrecke.
Tipp |
|
|---|---|
|
Ist nur die zurückgelegte Wegstrecke von Interesse, so kann diese auch durch rekursives
Aufrufen der Funktion |
|
Beispiel 2
Das Integral soll in einem Intervall von 20 Sekunden neu gestartet werden
Aufgabenstellung
Die Modulo-Funktion kann genutzt werden, um das Integral zurückzusetzen, da alle 20 Sekunden gilt T() mod 20 = 0.
Lösung
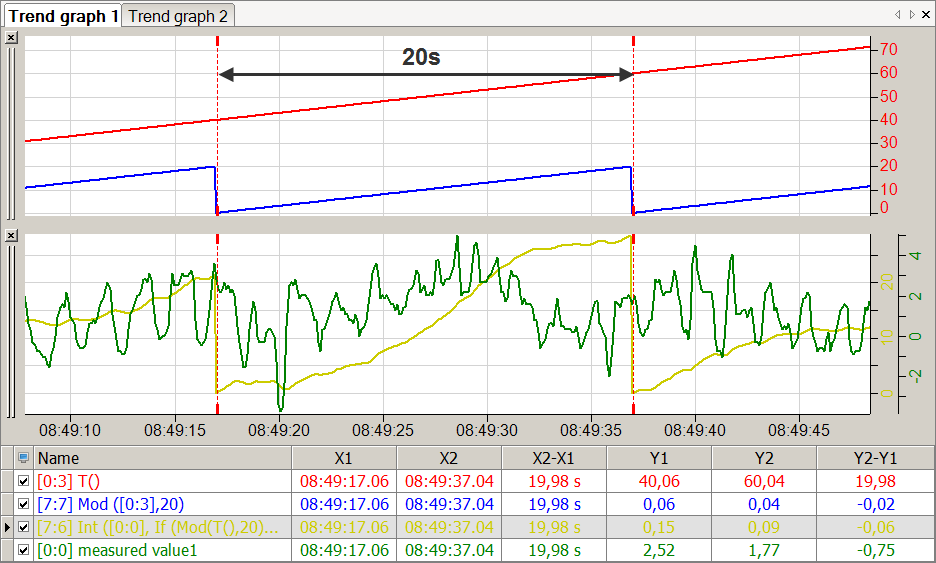
|
Rot |
Zeitfunktion |
Blau |
Modulo20 der Zeitfunktion |
|
Grün |
Messwert |
Gelb |
Integral des Messwertes mit 20 Sekunden-Reset |